History

The concept of a body so massive that not even light could escape it was put forward by the English geologist John Michell in a 1783 paper sent to the Royal Society. At that time, the Newtonian theory of gravity and the concept of escape velocity were well known. Michell computed that a body 500 times the radius of the Sun and of the same density would have, at its surface, an escape velocity equal to the speed of light, and therefore would be invisible. In his words:

If the semi-diameter of a sphere of the same density as the Sun were to exceed that of the Sun in the proportion of 500 to 1, a body falling from an infinite height towards it would have acquired at its surface greater velocity than that of light, and consequently supposing light to be attracted by the same force in proportion to its vis inertiae (inertial mass), with other bodies, all light emitted from such a body would be made to return towards it by its own proper gravity.

Although he thought it unlikely, Michell considered the possibility that many such objects that cannot be seen might be present in the cosmos.

In 1796, the French mathematician Pierre-Simon Laplace promoted the same idea in the first and second edition of his book Exposition du Systeme du Monde. It disappeared in later editions. The whole idea gained little attention in the 19th century, since light was thought to be a massless wave, not influenced by gravity.

In 1915, Einstein developed the theory of gravity called General Relativity. Earlier he had shown that gravity does influence light. A few months later, Karl Schwarzschild gave the solution for the gravitational field of a point mass, showing that something we now call a black hole could theoretically exist. The Schwarzschild radius is now known to be the radius of the event horizon of a non-rotating black hole, but this was not well understood at that time. Schwarzschild himself thought it not to be physical.

In the 1920s, Subrahmanyan Chandrasekhar argued that special relativity demonstrated that a non-radiating body above 1.44 solar masses, now known as the Chandrasekhar limit, would collapse since there was nothing known at that time that could stop it from doing so. His arguments were opposed by Arthur Eddington, who believed that something would inevitably stop the collapse. Both were correct, since a white dwarf more massive than the Chandrasekhar limit will collapse into a neutron star. However, a neutron star above about three solar masses will itself become unstable against collapse due to similar physics.

In 1939, Robert Oppenheimer and H. Snyder predicted that massive stars could undergo a dramatic gravitational collapse. Black holes could, in principle, be formed in nature. Such objects for a while were called frozen stars since the collapse would be observed to rapidly slow down and become heavily redshifted near the Schwarzschild radius. The mathematics showed that an outside observer would see the surface of the star frozen in time at the instant where it crosses that radius. However, these hypothetical objects were not the topic of much interest until the late 1960s. Most physicists believed that they were a peculiar feature of the highly symmetric solution found by Schwarzschild, and that objects collapsing in nature would not form black holes.

Interest in black holes was rekindled in 1967 because of theoretical and experimental progress, and the possibility of harnessing the immense gravitational energy of black holes for future space research. Stephen Hawking and Roger Penrose proved that black holes are a generic feature in Einstein's theory of gravity, and cannot be avoided in some collapsing objects. Interest was renewed in the astronomical community with the discovery of pulsars. Shortly thereafter, the use of the expression "black hole" was coined by theoretical physicist John Wheeler [1]. Prior to that time, the term black star was used occasionally. The latter term appears in an early episode of Star Trek, and was still used occasionally after 1967. This is because some people found the term "black hole" obscene when translated into Russian or French, for example. The older Newtonian objects of Michell and Laplace are often referred to as "dark stars" to distinguish them from the "black holes" of general relativity.

Evidence

Unsolved problems in physics: Do black holes really exist? If not, then what are the ultracompact massive objects that have been observed and what physics governs them?

A (simulated) Black Hole of ten solar masses as seen from a distance of 600km with the Milky Way in the background (horizontal camera opening angle: 90°).

Formation

General relativity (as well as most other metric theories of gravity) not only says that black holes can exist, but in fact predicts that they will be formed in nature whenever a sufficient amount of mass gets packed in a given region of space, through a process called gravitational collapse. For example, if you compressed the Sun to a radius of three kilometers, about four millionths of its present size, it would become a black hole. As the mass inside the given region of space increases, its gravity becomes stronger — or, in the language of relativity, the space around it becomes increasingly deformed. Eventually gravity gets so strong that nothing can escape, an event horizon is formed, and matter and energy must inevitably collapse into a singularity.

A quantitative analysis of this idea led to the prediction that a star remaining about three times the mass of the Sun at the end of its evolution, will almost inevitably shrink to the critical size needed to undergo a gravitational collapse. Once collapse starts, it cannot be stopped by any physical force, and a black hole is created. This is because there is a limit to the strength of materials due to the fact that the speed of sound, related to the materials stiffness, cannot be greater than the speed of light.

Stellar collapse will generate black holes containing at least three solar masses. Black holes smaller than this limit can only be created if their matter is subjected to sufficient pressure from some source other than self-gravitation. The enormous pressures needed for this are thought to have existed in the very early stages of the universe, possibly creating primordial black holes which could have masses smaller than that of the Sun.

Supermassive black holes are believed to exist in the centres of most, (if not all) galaxies, including our own Milky Way. This type of black hole contains millions to billions of solar masses, and there are several models of how they might have been formed. The first is via gravitational collapse of a dense cluster of stars. A second is by large amounts of mass accreting onto a "seed" black hole of stellar mass. A third is by repeated fusion of smaller black holes. Finally it may be possible to construct such a black hole by the collapse of a large gas cloud via an intermediate stage of a relativistic star.

Certain models of unification of the four fundamental forces allow the formation of micro black holes under laboratory conditions. These postulate that the energy at which gravity is unified with the other forces is comparable to the energy at which the other three are unified, as opposed to being the Planck energy (which is much higher). This would allow production of extremely short-lived black holes in terrestrial particle accelerators. No conclusive evidence of this type of black hole production has been presented, though even a negative result improves constraints on compactification of extra dimensions from string theory or other models of physics.

Observation

Formation of extragalactic jets from a black hole's accretion disk

In theory, no object beyond the event horizon of a black hole can ever escape, including light. However, black holes can be inductively detected from observation of phenomena near them, such as gravitational lensing, galactic jets, and stars that appear to be in orbit around space where there is no visible matter.

The most conspicuous effects are believed to come from matter accreting onto a black hole, which is predicted to collect into an extremely hot and fast-spinning accretion disk. The internal viscosity of the disk causes it to become extremely hot, and emit large amounts of X-ray and ultraviolet radiation. This process is extremely efficient and can convert about 50% of the rest mass energy of an object into radiation, as opposed to nuclear fusion which can only convert a few percent of the mass to energy. Other observed effects, are narrow jets of particles at relativistic speeds heading along the disk's axis.

However, accretion disks, jets, and orbiting objects are found not only around black holes, but also around other objects such as neutron stars and white dwarfs; and the dynamics of bodies near these non-black hole attractors is largely similar to that of bodies around black holes. It is currently a very complex and active field of research involving magnetic fields and plasma physics to disentangle what is going on. Hence, for the most part, observations of accretion disks and orbital motions merely indicate that there is a compact object of a certain mass, and says very little about the nature of that object. The identification of an object as a black hole requires the further assumption that no other object (or bound system of objects) could be so massive and compact. Most astrophysicists accept that this is the case, since according to general relativity, any concentration of matter of sufficient density must necessarily collapse into a black hole in an astrophysically short time scale.

One important observable difference between black holes and other compact massive objects is that any infalling matter will eventually collide with the latter at relativistic speeds, leading to emission as the kinetic energy of the matter is thermalised. In addition thermonuclear "burning" may occur on the surface as material builds up. These processes produce irregular intense flares of X-rays and other hard radiation. Thus the lack of such flare-ups around a compact concentration of mass is taken as evidence that the object is a black hole, with no surface onto which matter can collect.

Have we found them?

Location of the X-ray source Cygnus X-1 which is widely accepted to be a 10 solar mass black hole orbiting a blue giant star

There is now a great deal of indirect astronomical observational evidence for black holes in two mass ranges:

• stellar mass black holes with masses of a typical star (4–15 times the mass of our Sun), and
• supermassive black holes with masses ranging from of order 10⁵ to 10¹⁰ solar masses.

Additionally, there is some evidence for intermediate-mass black holes (IMBHs), those with masses of a few hundred to a few thousand times that of the Sun. These black holes may be responsible for the emission from Ultra Luminous X-ray Sources (ULX's).

Candidates for stellar-mass black holes were identified mainly by the presence of accretion disks of the right size and speed, without the irregular flare-ups that are expected from disks around other compact objects. Stellar-mass black holes may be involved in gamma ray bursts (GRBs), although observations of GRBs in association with supernovae or other objects that are not black holes [2] [3] have reduced the possibility of a link.

Candidates for more massive black holes were first provided by the active galactic nuclei and quasars, discovered by radioastronomers in the 1960s. The efficient conversion of mass into energy by friction in the accretion disk of a black hole seems to be the only explanation for the copious amounts of energy generated by such objects. Indeed the introduction of this theory in the 1970s removed a major objection to the belief that quasars were distant galaxies — namely, that no physical mechanism could generate that much energy.

From observations in the 1980s of motions of stars around the galactic centre, it is now believed that such supermassive black holes exist in the centre of most galaxies, including our own Milky Way. Sagittarius A* is now generally agreed to be the location of a supermassive black hole at the centre of the Milky Way galaxy. The orbits of stars within a few AU of Sagittarius A* rule out any object other than a black hole at the centre of the Milky Way assuming the current standard laws of physics are correct.

The jet emitted by the galaxy M87 in this image is thought to be caused by a supermassive black hole at the galaxy's centre

The current picture is that all galaxies may have a supermassive black hole in their centre, and that this black hole accretes gas and dust in the middle of the galaxies generating huge amounts of radiation — until all the nearby mass has been swallowed and the process shuts off. This picture also nicely explains why there are no nearby quasars.

Although the details are still not clear, it seems that the growth of the black hole is intimately related to the growth of the spheroidal component — an elliptical galaxy, or the bulge of a spiral galaxy — in which it lives. Interestingly, the Hubble Telescope has recently identified evidence indicating that intermediate size black holes exist in globular clusters. The observed globular clusters M15 and G1 do not orbit the Milky Way Galaxy. The evidence for the black holes stems from the orbital velocity of the stars about the globular clusters. Stars orbiting a compact high-density object will travel faster than they would otherwise in its absence. Another curious observation is that the black holes obey the same proportionality law as galactic black holes. That would be that the black hole is .5 percent the mass of the object.

Recent discoveries

In 2004 a cluster of black holes was detected, leading to new theories about the distribution of black holes in the universe; scientists now believe that there are close to five times as many black holes as previously predicted.

In July 2004 astronomers found a giant black hole, Q0906+6930, at the centre of a distant galaxy in the Ursa Major constellation. The size and presumed age of the black hole has implications that may determine the age of the universe [4].

In November 2004 a team of astronomers reported the discovery of the first intermediate-mass black hole in our Galaxy, orbiting three light-years from Sagittarius A*. This medium black hole of 1,300 solar masses is within a cluster of seven stars, possibly the remnant of a massive star cluster that has been stripped down by the Galactic Centre (Nature News) (original article). This observation may add support to the idea that supermassive black holes grow by absorbing nearby smaller black holes and stars.

In February 2005, a blue giant star SDSS J090745.0+24507 was found to be leaving the Milky Way at twice the escape velocity (0.0022 of the speed of light). The path of the star can be traced back to the galactic core. The high velocity of this star supports the hypothesis of a super-massive black hole in the centre of the galaxy.

The formation of micro black holes on Earth in particle accelerators has been tentatively reported, (see, for example, [5]) but not yet confirmed. So far there are no observed candidates for primordial black holes.

Features and issues

Black holes require the general relativistic concept of a curved spacetime: their most striking properties rely on a distortion of the geometry of the space surrounding them.

The event horizon

The "surface" of a black hole is the so-called event horizon, an imaginary surface surrounding the mass of the black hole. Stephen Hawking proved that the topology of the event horizon of a (four dimensional) black hole is a 2-sphere. At the event horizon, the escape velocity is equal to the speed of light. Thus, anything inside the event horizon, including a photon, is prevented from escaping across the event horizon by the extremely strong gravitational field. Particles from outside this region can fall in, cross the event horizon, and will never be able to leave.

According to classical general relativity, black holes can be entirely characterised according to three parameters: mass, angular momentum, and electric charge. This principle is summarised by the saying, coined by John Wheeler, "black holes have no hair".

Objects in a gravitational field experience a slowing down of time, called time dilation. This phenomenon has been verified experimentally in the Scout rocket experiment of 1976 [6], and is, for example, taken into account in the GPS system. Near the event horizon, the time dilation increases rapidly. From the point of view of an external observer, it takes an infinite amount of time for an object to approach the event horizon, at which point the light coming from it is infinitely red-shifted. To the distant observer, the object, falling slower and slower, approaches but never reaches the event horizon. However, the object itself might not even notice the point at which it crosses the event horizon, and will do so in a finite amount of proper time.

The singularity

At the centre of the black hole, well inside the event horizon, general relativity predicts a singularity, a place where the curvature of spacetime becomes infinite and gravitational forces become infinitely strong. Spacetime inside the event horizon of an uncharged non-rotating black hole is peculiar in that the singularity is in every observer's future, so all particles within the event horizon move inexorably towards it (Penrose and Hawking). This means that there is a conceptual inaccuracy in the nonrelativistic concept of a black hole as originally proposed by John Michell in 1783. In Michell's theory, the escape velocity equals the speed of light, but it would still, for example, be theoretically possible to hoist an object out of a black hole using a rope. General relativity eliminates such loopholes, because once an object is inside the event horizon, its time-line contains an end-point to time itself, and no possible world-lines come back out through the event horizon.

It is expected that future refinements or generalisations of general relativity (in particular quantum gravity) will change what is thought about the nature of black hole interiors. Most theorists interpret the mathematical singularity of the equations as indicating that the current theory is not complete, and that new phenomena must come into play as one approaches the singularity.

The question may be largely academic, as the cosmic censorship hypothesis asserts that there are no naked singularities in general relativity. This hypothesis is that every singularity is hidden behind an event horizon and cannot be probed. However, whether this hypothesis is true or not remains controversial and an active area of theoretical research.

Another school of thought[7] holds that no singularity occurs, because of a bubble-like local inflation in the interior of the collapsing star. Radii stop converging as they approach the event horizon, are parallel at the horizon, and begin diverging in the interior. The solution resembles a wormhole (from the exterior to the interior) in a neighbourhood of the horizon, with the horizon as the neck.

Entering a black hole

A black hole's gravity as described by the Theory of Relativity causes a number of peculiar effects. An object approaching a simple Schwarzschild-type (non-rotating) black hole's centre will appear to distant observers as having an increasingly slow descent as the object approaches the event horizon. Because of the peculiar effects of Relativity, local space in the vicinity of the black hole is "stretched", constantly increasing the distance required to escape the gravitational field, thus photons take much longer to exit the closer they are created to the event horizon. The light does not slow down when escaping the gravity well but instead experiences a redshift.

From the object's frame of reference, it will cross the event horizon and reach the singularity, at the centre of the black hole within a finite amount of time. Once the object crosses over the event horizon, light it emits will no longer escape the black hole, and the object can no longer be observed by an observer outside of the event horizon. As the object continues to approach the singularity, it will be stretched radially with respect to the black hole and compressed in directions perpendicular to this axis. This phenomenon, called spaghettification, occurs as a result of tidal forces: the parts of the object closer to the singularity feel a stronger pull towards it (causing stretching along the axis), and all parts are pulled in the direction of the singularity, which is only aligned with the object's average motion along the axis of the object (causing compression towards the axis).

Rotating black holes

See the page "rotating black hole" for detailed information

An artist's impression of a black hole with a closely orbiting companion star that exceeds its Roche limit. In-falling matter forms an accretion disk, with some of the matter being ejected in highly energetic polar jets.

According to theory, the event horizon of a black hole that is not spinning is spherical, and its singularity is (informally speaking) a single point. If the black hole carries angular momentum (inherited from a star that is spinning at the time of its collapse), it begins to drag space-time surrounding the event horizon in an effect known as frame-dragging. This spinning area surrounding the event horizon is called the ergosphere and has an ellipsoidal shape. Since the ergosphere is located outside the event horizon, objects can exist within the ergosphere without falling into the hole. However, because space-time itself is moving in the ergosphere, it is impossible for objects to remain in a fixed position. Objects grazing the ergosphere could in some circumstances be catapulted outwards at great speed, extracting energy (and angular momentum) from the hole, hence the name ergosphere ("sphere of work") because it is capable of doing work.

The singularity inside a rotating black hole is a ring. It is possible for an observer to avoid hitting this singularity, by for example, proceding along the black hole spin axis. However, it is still not possible to escape the black hole's event horizon, and the observer is trapped inside.

Entropy and Hawking radiation

In 1971, Stephen Hawking showed that the total area of the event horizons of any collection of classical black holes can never decrease. This sounded remarkably similar to the Second Law of Thermodynamics, with area playing the role of entropy. Classically, one could violate the second law of thermodynamics by material entering a black hole disappearing from our universe and resulting in a decrease of the total entropy of the universe. Therefore, Jacob Bekenstein proposed that a black hole should have an entropy and that it should be proportional to its horizon area. Since black holes do not classically emit radiation, the thermodynamic viewpoint was simply an analogy. However, in 1974, Hawking applied quantum field theory to the curved spacetime around the event horizon and discovered that black holes can emit thermal radiation, known as Hawking radiation. Using the first law of black hole mechanics, it follows that the entropy of a black hole is one quarter of the area of the horizon. This is a universal result and can be extended to apply to cosmological horizons such as in de Sitter space. It was later suggested that black holes are maximum-entropy objects, meaning that the maximum entropy of a region of space is the entropy of the largest black hole that can fit into it. This led to the holographic principle.

Hawking radiation originates just outside the event horizon and, so far as it is understood, does not carry information from its interior since it is thermal. However, this means that black holes are not completely black: the effect implies that the mass of a black hole slowly evaporates with time. Although these effects are negligible for astronomical black holes, they are significant for hypothetical very small black holes where quantum-mechanical effects dominate. Indeed, small black holes are predicted to undergo runaway evaporation and eventually vanish in a burst of radiation. Hence, every black hole that cannot consume new mass has a finite life that is directly related to its mass.

The original derivation of Hawking radiation did not take into account the back-reaction due to the loss of energy of the hole. This effect may add small corrections to the spectrum, altering it from pure black body radiation. The correction terms for the entropy are logarithmic in the hole area compared to the linear dominant term. The coefficents of the sub-linear corrections to the entropy formula are currently contested in the literature due to the current poor understanding of quantum gravity.

Black hole unitarity

An open question in fundamental physics is the so-called information loss paradox, or black hole unitarity paradox. Classically, the laws of physics are the same run forward or in reverse. That is, if the position and velocity of every particle in the universe were measured, we could (disregarding chaos) work backwards to discover the history of the universe arbitrarily far in the past. In quantum mechanics, this corresponds to a vital property called unitarity which has to do with the conservation of probability.

Black holes, however, violate this rule. Because of the no hair theorem, we can never determine what went into the black hole. Information is apparently destroyed, as there is no way to reconstruct what went into the black hole. This is an important unsolved conceptual problem in quantum gravity.

On 21 July 2004 Stephen Hawking presented a new argument that black holes do eventually emit information about what they swallow, reversing his previous position on information loss. He proposed that quantum perturbations of the event horizon could allow information to escape from a black hole, where it can influence subsequent Hawking radiation [8]. The theory has not yet been reviewed by the scientific community, and if it is accepted it is likely to resolve the black hole information paradox. In the meantime, the announcement has attracted a lot of attention in the media.

Mathematical theory

An artist depiction of a two black holes merging.

Black holes are predictions of Albert Einstein's theory of general relativity. In particular, they occur in the Schwarzschild metric, one of the earliest and simplest solutions to Einstein's equations, found by Karl Schwarzschild in 1915. This solution describes the curvature of spacetime in the vicinity of a static and spherically symmetric object, where the metric is

,

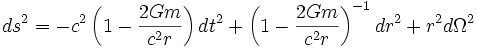where 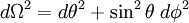is a standard element of solid angle.

According to Schwarzschild's solution, a gravitating object will collapse into a black hole if its radius is smaller than a characteristic distance, known as the Schwarzschild radius. Below this radius, spacetime is so strongly curved that any light ray emitted in this region, regardless of the direction in which it is emitted, will travel towards the centre of the system. Because relativity forbids anything from travelling faster than light, anything below the Schwarzschild radius – including the constituent particles of the gravitating object – will collapse into the centre. A gravitational singularity, a region of theoretically infinite density, forms at this point. Because not even light can escape from within the Schwarzschild radius, a classical black hole would truly appear black.

The Schwarzschild radius is given by

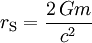
where G is the gravitational constant, m is the mass of the object, and c is the speed of light. For an object with the mass of the Earth, the Schwarzschild radius is a mere 9 millimeters — about the size of a marble.

The mean density inside the Schwarzschild radius decreases as the mass of the black hole increases, so while an earth-mass black hole would have a density of 2 × 10³⁰ kg/m³, a supermassive black hole of 10⁹ solar masses has a density of around 20 kg/m³, less than water! The mean density is given by

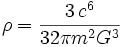
Since the Earth has a mean radius of 6371 km, its volume would have to be reduced 4 × 10²⁶ times to collapse into a black hole. For an object with the mass of the Sun, the Schwarzschild radius is approximately 3 km, much smaller than the Sun's current radius of about 700,000 km. It is also significantly smaller than the radius to which the Sun will ultimately shrink after exhausting its nuclear fuel, which is several thousand kilometers. More massive stars can collapse into black holes at the end of their lifetimes.

More general black holes are also predicted by other solutions to Einstein's equations, such as the Kerr metric for a rotating black hole, which possesses a ring singularity. Then we have the Reissner-Nordström metric for charged black holes. Last the Kerr-Newman metric is for the case of a charged and rotating black hole.

There is also the Black Hole Entropy formula:

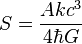
Where A is the area of the event horizon of the black hole, 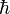is Dirac's constant (the "reduced Planck constant"), k is the Boltzmann constant, G is the gravitational constant, c is the speed of light and S is the entropy.

A convenient length scale to measure black hole processes is the "gravitational radius", which is equal to

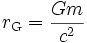
When expressed in terms of this length scale, many phenomena appear at integer radii. For example, the radius of a Schwarzschild black hole is two gravitational radii and the radius of a maximally rotating Kerr black hole is one gravitational radius. The location of the light circularization radius around a Schwarzschild black hole (where light may orbit the hole in an unstable circular orbit) is 3r_G. The location of the marginally stable orbit, thought to be close to the inner edge of an accretion disk, is at 6r_G for a Schwarzschild black hole.

Alternative models

Several alternate models, which behave like a black hole but avoid the singularity, are considered. But most researchers judge these concepts artificial, as they are more complicated but don't give near term observable differences from black holes (see Occam's razor). The most prominent theory is the Gravastar.

In March 2005, physicist George Chapline at the Lawrence Livermore National Laboratory in California proposed that black holes do not exist, and that objects currently thought to be black holes are actually dark-energy stars. He draws this conclusion from some quantum mechanical analyses. Although his proposal currently has little support in the physics community, it was widely reported by the media (report in Nature News) (original article).