Theories

The giant impact hypothesis (or Big Splash or Big Whack; cf. Big Bang) is the now dominant scientific theory for the formation of the Moon, which is thought to have formed as a result of a collision between the young Earth and a Mars-sized body sometimes called Theia. The original hypothesis was first proposed in a paper published in Icarus in 1975 by Dr. William K. Hartmann and Dr. Donald R. Davis.

According to the hypothesis, 4.533 billion years (4.533 Ga) ago, shortly after the formation of the Earth, a Mars-sized planetesimal hit the Earth at an oblique angle, destroying the impactor and ejecting most of that body along with a significant portion of the Earth's felsic-rich mantle out into space. Some of this material then coalesced into the Moon from an orbiting ring of debris. Current estimates based on computer simulations of such an event suggest the spherical shape of the moon was attained between one and one hundred years after the impact.

Simulation of impact and formation of the moon

Evidence for this impact comes from rocks collected during the Apollo Moon landings, which show an oxygen isotope composition that is nearly identical to the Earth's mantle. Chemical inspection of those rocks found them to be nearly devoid of volatile and lighter elements, leading to the inference that they formed from an unusually extreme amount of heating that boiled them off. Seismometers on the Moon have measured the size of its nickel-iron core and have found that it is much smaller than predicted under other formation scenarios, such as tandem formation with the Earth. A smaller core is consistent with the impact hypothesis because it predicts that the Moon was formed mostly from the mantle of the Earth and partly from the mantle of the impacting body and not from the core of the impacting body (it is thought that the core of the impactor sank and merged with the Earth's core).

Other than the existence of the Moon itself, the primary legacy of this event, say researchers, is the fact that the Earth does not have enough of the lighter-colored felsic and intermediate rock-types to completely cover its entire surface. Thus we have continents made from felsic rocks and ocean basins which are made of the darker-colored, heavier and more metal-rich mafic rock types. This difference in composition along with the presence of water allows for an extensively active system of plate tectonics on the Earth. Others have postulated that the axial-tilt and initial rotation of the Earth had their origin at this time.

Animation of Theia forming in Earth's L₅ point and then drifting into impact. The animation progresses in one-year steps making Earth appear not to move. The view is of the south pole.

The apparent improbability of a Mars-sized body hitting the Earth at exactly the correct angle to avoid completely destroying the planet, combined with the fortunate degree of axial-tilt that this event set up (thus allowing for seasons), and for making possible vigorous plate tectonics on the Earth (which is vital to the carbon cycle) has been put forward by some to explain the apparent rarity of life in the universe (the Fermi Paradox). This idea is called the Rare Earth hypothesis. However, in a recent article Edward Belbruno and Richard Gott III argue that an impact body could have formed at the Lagrangian point L₄ or L₅, and then drifted into a chaotic orbit that would impact the Earth with a suitably low velocity; this mechanism would allow for such impact events with a significantly increased probability.

Simulation work published in 2005 by Robin Canup suggested that Pluto's largest moon Charon could also have formed by a giant impact around 4.5 billion years ago, in this case by another Kuiper belt object between 1600 and 2000 kilometres in diameter that struck the planet at a speed of 1 kilometre per second. Canup speculated that this process of moon formation could have been common in the early solar system.

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Space-Time Theory:

In physics, spacetime is a model that combines 3-D space and 1-D time into a single construct called the space-time continuum (the 4th dimension). According to Euclidean space perception, our universe has three dimensions of space, and one dimension of time. By combining the two concepts into a single manifold, physicists are able to deal in a unified way with spacetimes which attempt to explain the workings of the universe at both supergalactic and subatomic levels. There may be an endless number of dimensions, though 4-D spacetime is as far as modern-day scientists know.

Treating space and time on the same footing and as two aspects of a unified whole was devised by Hermann Minkowski shortly after the theory of special relativity was developed by Albert Einstein. This unification is further exemplified by the common practice shown by specialists of expressing time in the same units as space by multiplying time measurements by the speed of light. The concept of spacetime is vital to this theory and also to general relativity, an extension of special relativity, that takes into account gravitation.

Space-times are the arenas in which all physical events take place — for example, the motion of planets around the Sun may be described in a particular type of space-time, or the motion of light around a rotating star may be described in another type of space-time. In any given spacetime, an event is a unique position at a unique time.

Basic concepts

The basic elements of spacetime are events, these being represented by points in the spacetime. Examples of events include the explosion of a star, or the single beat of a drum.

A spacetime is independent of any observer. However, in describing physical phenomena (which occur at certain moments of time in a given region of space), each observer chooses a convenient coordinate system. Events are specified by four real numbers in any coordinate system.

The worldline of a particle or light beam is the path that this particle or beam takes in the spacetime and represents the history of the particle or beam. Certain types of worldlines, called geodesics (of the spacetime), are the shortest paths between any two events. Geodesic motion may be thought of as "pure motion" (inertial motion) in spacetime, that is, free from any external influences.

Spacetime intervals

The new concept of spacetime brings with it a new concept of distance. Whereas distances are always positive in Euclidean space, the distance between any two events in spacetime (called an interval) may be positive, zero, or negative. The spacetime interval quantifies this new distance (in Cartesian coordinates $x, y, z, t$ ):

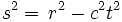
$s^2 = \, r^2 - c^2 t^2$

where $c$ is the speed of light, differences of the space and time coordinates of the two events are denoted by $r$ and $t$ , respectively and $r 2 = x 2 + y 2 + z 2$ .

Pairs of events in spacetime may be classified into 3 distinct types based on 'how far' apart they are:

time-like (more than enough time passes for there to be a cause-effect relationship between the two events; $s 2 < 0$ ).
light-like (the space between the two events is exactly balanced by the time between the two events; $s 2 = 0$ ).
space-like (not enough time passes for there to be a cause-effect relationship between the two events; $s 2 > 0$ ).

Events with a positive space-time interval are in each other's future or past, and the value of the interval defines the proper time measured by an observer traveling between them. Events with a spacetime interval of zero are separated by the propagation of a light signal.

Mathematics of space-times

For physical reasons, a space-time continuum is mathematically defined as a four-dimensional, smooth, connected pseudo-Riemannian manifold together with a smooth, Lorentz metric of signature $\left(3,1\right)$ . The metric determines the geometry of spacetime, as well as determining the geodesics of particles and light beams. About each point (event) on this manifold, coordinate charts are used to represent observers in reference frames. Usually, Cartesian coordinates $\left(x, y, z, t\right)$ are used.

A reference frame (observer) being identified with one of these coordinate charts, any observer can describe any event $p$ . Another reference frame may be identified by a second coordinate chart about $p$ . Two observers (one in each reference frame) may describe the same event $p$ but obtain different descriptions.

Usually, many overlapping coordinate charts are needed to cover a manifold. Given two coordinate charts, one containing $p$ (representing an observer) and another containing $q$ (another observer), the intersection of the charts represents the region of spacetime in which both observers can measure physical quantities and hence compare results. The relation between the two sets of measurements is given by a non-singular coordinate transformation on this intersection. The idea of coordinate charts as 'local observers who can perform measurements in their vicinity' also makes good physical sense, as this is how one actually collects physical data - locally.

For example, two observers, one of whom is on Earth, but the other one who is on a fast rocket to Jupiter, may observe a comet crashing into Jupiter (this is the event $p$ ). In general, they will disagree about the exact location and timing of this impact, i.e., they will have different 4-tuples $\left(x, y, z, t\right)$ (as they are using different coordinate systems). Although their kinematic descriptions will differ, dynamical (physical) laws, such as momentum conservation and the first law of thermodynamics, will still hold. In fact, relativity theory requires more than this in the sense that it stipulates these (and all other physical) laws must take the same form in all coordinate systems. This introduces tensors into relativity, by which all physical quantities are represented.

Geodesics are said to be timelike, null, or spacelike if the tangent vector to one point of the geodesic is of this nature. The paths of particles and light beams in spacetime are represented by timelike and null (light-like) geodesics (respectively).

Space-time topologyThe assumptions contained in the definition of a spacetime are usually justified by the following considerations:

The connectedness assumption serves two main purposes. Firstly, different observers making measurements (represented by coordinate charts) should be able compare their observations on the non-empty intersection of the charts. If the connectedness assumption were dropped, this would not be possible. Secondly, for a manifold, the property of connectedness and path-connectedness are equivalent and one requires the existence of paths (in particular, geodesics) in the spacetime to represent the motion of particles and radiation.

Every spacetime is paracompact. This property, allied with the smoothness of the spacetime, gives rise to a (smooth) linear connection, an important structure in general relativity. Some important theorems on constructing spacetimes from compact and non-compact manifolds include the following:

A compact manifold can be turned into a spacetime if, and only if, its Euler characteristic is 0.
Any non-compact 4-manifold can be turned into a spacetime.

Space-time continua and symmetry

For further details, see the article spacetime symmetries

Often in general relativity, space-time continua that have some form of symmetry are studied. Some of the most popular ones include:

Spacetime in special relativity

The geometry of spacetime in special relativity is described by the Minkowski metric on R⁴. This spacetime is called Minkowski space. The Minkowski metric is usually denoted by $η$ and can be written as a 4 by 4 matrix:

$\eta_{ab} \, = diag(-1, 1, 1, 1)$

where the Landau-Lifshitz spacelike convention is being used. A basic assumption of relativity is that coordinate transformations must leave spacetime intervals invariant. Intervals are invariant under Lorentz transformations. This invariance property leads to the use of four-vectors (and other tensors) in describing physics.

Strictly speaking one can also consider events in Newtonian physics as a single spacetime. This is Galilean-Newtonian relativity, and the coordinate systems are related by Galilean transformations. However, since these preserve spatial and temporal distances independently, such a space-time can be decomposed into spatial coordinates plus temporal coordinates, which is not possible in the general case.

Spacetime in general relativity

In general relativity, it is assumed that spacetime is curved by the presence of matter (energy), this curvature being represented by the Riemann tensor. In special relativity, the Riemann tensor is identically zero, and so this concept of 'non-curvedness' is sometimes expressed by the statement: 'Minkowski space is flat'.

Many space-time continua have physical interpretations which most physicists would consider bizarre or unsettling. For example, a compact spacetime has closed timelike curves, which violate our usual ideas of causality (that is, "future" events could affect "past" ones). For this reason, mathematical physicists usually consider only restricted subsets of all the possible spacetimes. One way to do this is to study "realistic" solutions of the equations of general relativity. Another way is add some additional "physically reasonable" but still fairly general geometric restrictions, and try to prove interesting things about the resulting spacetimes. The latter approach has led to some important results, most notably the Penrose-Hawking singularity theorems.

World line of the orbit of the Earth depicted in two spatial dimensions X and Y (the plane of the Earth orbit) and a time dimension, usually put as the vertical axis. Note that the orbit of the Earth is (almost) a circle in space, but its worldline is a helix in spacetime.

=====================================================================

Big-Bang Theory

In physical cosmology, the Big Bang is the scientific theory that the universe emerged from an enormously dense and hot state about 13.7 billion years ago. The Big Bang theory is based on the observed Hubble's law redshift of distant galaxies that when taken together with the cosmological principle indicate that space is expanding according to the Friedmann-Lemaître model of general relativity. Extrapolated into the past, these observations show that the universe has expanded from a state in which all the matter and energy in the universe was at an immense temperature and density. Physicists do not widely agree on what happened before this, although general relativity predicts a gravitational singularity (for reporting on some of the more notable speculation on this issue, see cosmogony).

The term Big Bang is used both in a narrow sense to refer to a point in time when the observed expansion of the universe (Hubble's law) began — calculated to be 13.7 billion (1.37 × 10¹⁰) years ago (±2%) — and in a more general sense to refer to the prevailing cosmological paradigm explaining the origin and expansion of the universe, as well as the composition of primordial matter through nucleosynthesis as predicted by the Alpher-Bethe-Gamow theory ^[1].

One consequence of the Big Bang is that the conditions of today's universe are different from the conditions in the past or in the future (natural evolution of universe constantly takes place). From this model, George Gamow in 1948 was able to predict, at least qualitatively, the existence of cosmic microwave background radiation (CMB) ^[2]. The CMB was discovered in the 1960s and further validated the Big Bang theory over its chief rival, the steady state theory.

History

Main article: History of the Big Bang

The Big Bang theory developed from observations and theoretical considerations. Observationally, it was determined that most spiral nebulae were receding from Earth, but those who made the observation weren't aware of the cosmological implications, nor that the supposed nebulae were actually galaxies outside our own Milky Way^[3]. In 1927, Georges Lemaître independently derived the Friedmann-Lemaître-Robertson-Walker equations from Albert Einstein's equations of general relativity and proposed, on the basis of the recession of spiral nebulae, that the universe began with the "explosion" of a "primeval atom"—what was later called the Big Bang^[4]. Given the cosmological principle whereby the universe, when viewed on sufficiently large distance scales, has no preferred directions or preferred places, Hubble's law suggested that the universe was expanding contradicting the infinite and unchanging static universe scenario developed by Einstein.

This idea allowed for two opposing possibilities. One was Lemaître's Big Bang theory, advocated and developed by George Gamow. The other possibility was Fred Hoyle's steady state model in which new matter would be created as the galaxies moved away from each other. In this model, the universe is roughly the same at any point in time^[5]. It was actually Hoyle who coined the name of Lemaître's theory, referring to it sarcastically as "this big bang idea" during a program broadcast on March 28, 1949 by the BBC Third Programme. Hoyle repeated the term in further broadcasts in early 1950, as part of a series of five lectures entitled The Nature of Things. The text of each lecture was published in The Listener a week after the broadcast, the first time that the term "big bang" appeared in print. [1]

For a number of years the support for these theories was evenly divided. However, the observational evidence began to support the idea that the universe evolved from a hot dense state. Since the discovery of the cosmic microwave background radiation in 1965 it has been regarded as the best theory of the origin and evolution of the cosmos. Virtually all theoretical work in cosmology now involves extensions and refinements to the basic Big Bang theory. Much of the current work in cosmology includes understanding how galaxies form in the context of the Big Bang, understanding what happened at the Big Bang, and reconciling observations with the basic theory.

Huge advances in Big Bang cosmology were made in the late 1990s and the early 21st century as a result of major advances in telescope technology in combination with large amounts of satellite data such as that from COBE, the Hubble Space Telescope and WMAP. Such data has allowed cosmologists to calculate many of the parameters of the Big Bang to a new level of precision and led to the unexpected discovery that the expansion of the universe appears to be accelerating. (See dark energy.)

Overview

A graphical timeline is available here:

Graphical timeline of the Big Bang

Based on measurements of the expansion of the universe using Type Ia supernovae, measurements of the lumpiness of the cosmic microwave background, and measurements of the correlation function of galaxies, the universe has a calculated age of 13.7 ± 0.2 billion years. The agreement of these three independent measurements is considered strong evidence for the so-called ΛCDM model that describes the detailed nature of the contents of the universe.

The early universe was filled homogeneously and isotropically with an incredibly high energy density and concomitantly huge temperatures and pressures. It expanded and cooled, going through phase transitions analogous to the condensation of steam or freezing of water as it cools, but related to elementary particles.

Approximately 10^-35 seconds after the Planck epoch a phase transition caused the universe to experience exponential growth during a period called cosmic inflation. After inflation stopped, the material components of the universe were in the form of a quark-gluon plasma (also including all other particles—and perhaps experimentally produced recently as a quark-gluon liquid [2]) in which the constituent particles were all moving relativistically. As the universe continued growing in size, the temperature dropped. At a certain temperature, by an as-yet-unknown transition called baryogenesis, the quarks and gluons combined into baryons such as protons and neutrons, somehow producing the observed asymmetry between matter and antimatter. Still lower temperatures led to further symmetry breaking phase transitions that put the forces of physics and elementary particles into their present form. Later, some protons and neutrons combined to form the universe's deuterium and helium nuclei in a process called Big Bang nucleosynthesis. As the universe cooled, matter gradually stopped moving relativistically and its rest mass energy density came to gravitationally dominate that of radiation. After about 300,000 years the electrons and nuclei combined into atoms (mostly hydrogen); hence the radiation decoupled from matter and continued through space largely unimpeded. This relic radiation is the cosmic microwave background.

Over time, the slightly denser regions of the nearly uniformly distributed matter gravitationally attracted nearby matter and thus grew even denser, forming gas clouds, stars, galaxies, and the other astronomical structures observable today. The details of this process depend on the amount and type of matter in the universe. The three possible types are known as cold dark matter, hot dark matter, and baryonic matter. The best measurements available (from WMAP) show that the dominant form of matter in the universe is cold dark matter. The other two types of matter make up less than 20% of the matter in the universe.

The universe today appears to be dominated by a mysterious form of energy known as dark energy. Approximately 70% of the total energy density of today's universe is in this form. This component of the universe's composition is revealed by its property of causing the expansion of the universe to deviate from a linear velocity-distance relationship by causing spacetime to expand faster than expected at very large distances. Dark energy in its simplest formation takes the form of a cosmological constant term in Einstein's field equations of general relativity, but its composition is unknown and, more generally, the details of its equation of state and relationship with the standard model of particle physics continue to be investigated both observationally and theoretically.

All these observations are encapsulated in the ΛCDM model of cosmology, which is a mathematical model of the Big Bang with six free parameters. Mysteries appear as one looks closer to the beginning, when particle energies were higher than can yet be studied by experiment. There is no compelling physical model for the first 10^-33 seconds of the universe, before the phase transition called for by grand unification theory. At the "first instant", Einstein's theory of gravitation predicts a gravitational singularity where densities become infinite. To resolve this paradox, a theory of quantum gravitation is needed. Understanding this period of the history of the universe is one of the greatest unsolved problems in physics.

Theoretical underpinnings

As it stands today, the Big Bang is dependent on three assumptions:

When first developed, these ideas were simply taken as postulates, but today there are efforts underway to test each of them. Tests of the universality of physical laws have found that the largest possible deviation of the fine structure constant over the age of the universe is of order 10^-5^[6]. The isotropy of the universe that defines the Cosmological Principle has been tested to a level of 10^-5 and the universe has been measured to be homogeneous on the largest scales to the 10% level^[7]. There are efforts underway to test the Copernican Principle by means of looking at the interaction of galaxy groups and clusters with the CMB through the Sunyaev-Zel'dovich effect to a level of 1% accuracy^[8].

The Big Bang theory uses Weyl's postulate to unambiguously measure time at any point as the "time since the Planck epoch". Measurements in this system rely on conformal coordinates in which so-called comoving distances and conformal times remove the expansion of the universe, parameterized by the cosmological scale factor, from consideration of spacetime measurements. The comoving distances and conformal times are defined so that objects moving with the cosmological flow are always the same comoving distance apart and the particle horizon or observational limit of the local universe is set by the conformal time.

As the universe can be described by such coordinates, the Big Bang is not an explosion of matter moving outward to fill an empty universe; what is expanding is spacetime itself. It is this expansion that causes the physical distance between any two fixed points in our universe to increase. Objects that are bound together (for example, by gravity) do not expand with spacetime's expansion because the physical laws that govern them are assumed to be uniform and independent of the metric expansion. Moreover, the expansion of the universe on today's local scales is so small that any dependence of physical laws on the expansion is unmeasurable by current techniques.

Observational evidence

It is generally stated that there are three observational pillars that support the Big Bang theory of cosmology. These are the Hubble-type expansion seen in the redshifts of galaxies, the detailed measurements of the cosmic microwave background, and the abundance of light elements. (See Big Bang nucleosynthesis.) Additionally, the observed correlation function of large-scale structure of the cosmos fits well with standard Big Bang theory.

Hubble's law expansionMain article: Hubble's law

Observations of distant galaxies and quasars show that these objects are redshifted, meaning that the light emitted from them has been shifted to longer wavelengths. This is seen by taking a frequency spectrum of the objects and then matching the spectroscopic pattern of emission lines or absorption lines corresponding to atoms of the chemical elements interacting with the light. From this analysis, a redshift corresponding to a Doppler shift for the radiation can be measured which is explained by a recessional velocity. When the recessional velocities are plotted against the distances to the objects, a linear relationship, known as Hubble's law, is observed:

$v = H_0 D \,$

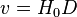
where

v

is the recessional velocity of the galaxy or other distant object

D

is the distance to the object and

H 0

is Hubble's constant, measured to be (71 ± 4) km/s/Mpc by the WMAP probe ^[9].

The Hubble's law observation has two possible explanations. One is that we are at the center of an explosion of galaxies, a position which is untenable given the Copernican principle. The second explanation is that the universe is uniformly expanding everywhere as a unique property of spacetime. This type of universal expansion was developed mathematically in the context of general relativity well before Hubble made his analysis and observations, and it remains the cornerstone of the Big Bang theory as developed by Friedmann-Lemaître-Robertson-Walker.

Cosmic microwave background radiation

Main article: Cosmic microwave background radiation

WMAP image of the cosmic microwave background radiation

The Big Bang theory predicted the existence of the cosmic microwave background radiation or CMB which is composed of photons emitted during baryogenesis. Because the early universe was in thermal equilibrium, the temperature of the radiation and the plasma were equal until the plasma recombined. Before atoms formed, radiation was constantly absorbed and reemitted in a process called Compton scattering: the early universe was opaque to light. However, cooling due to the expansion of the universe allowed the temperature to eventually fall below 3,000 K at which point electrons and nuclei combined to form atoms and the primordial plasma turned into a neutral gas. This is known as photon decoupling. A universe with only neutral atoms allows radiation to travel largely unimpeded.

Because the early universe was in thermal equilibrium, the radiation from this time had a blackbody spectrum and freely streamed through space until today, becoming redshifted because of the Hubble expansion. This reduces the high temperature of the blackbody spectrum. The radiation should be observable at every point in the universe to come from all directions of space.

In 1964, Arno Penzias and Robert Wilson, while conducting a series of diagnostic observations using a new microwave receiver owned by Bell Laboratories, discovered the cosmic background radiation. Their discovery provided substantial confirmation of the general CMB predictions—the radiation was found to be isotropic and consistent with a blackbody spectrum of about 3 K —and it pitched the balance of opinion in favor of the Big Bang hypothesis. Penzias and Wilson were awarded the Nobel Prize for their discovery.

In 1989, NASA launched the Cosmic Background Explorer satellite (COBE), and the initial findings, released in 1990, were consistent with the Big Bang's predictions regarding the CMB. COBE found a residual temperature of 2.726 K and determined that the CMB was isotropic to about one part in 10⁵^[10]. During the 1990s, CMB anisotropies were further investigated by a large number of ground-based experiments and the universe was shown to be almost geometrically flat by measuring the typical angular size (the size on the sky) of the anisotropies. (See shape of the universe.)

In early 2003 the results of the Wilkinson Microwave Anisotropy satellite (WMAP) were released, yielding what were at the time the most accurate values for some of the cosmological parameters. (see cosmic microwave background radiation experiments). This satellite also disproved several specific cosmic inflation models, but the results were consistent with the inflation theory in general.

Abundance of primordial elements

Main article: Big Bang nucleosynthesis

Using the Big Bang model it is possible to calculate the concentration of helium-4, helium-3, deuterium and lithium-7 in the universe as ratios to the amount of ordinary hydrogen, H. All the abundances depend on a single parameter, the ratio of photons to baryons. The ratios predicted (by mass, not by number) are about 0.25 for ⁴He/H, about 10^-3 for ²H/H, about 10^-4 for ³He/H and about 10^-9 for ⁷Li/H.

The measured abundances all agree with those predicted from a single value of the baryon-to-photon ratio. The agreement is relatively poor for ⁷Li and ⁴He, the two elements for which the systematic uncertainties are least understood. This is considered strong evidence for the Big Bang, as the theory is the only known explanation for the relative abundances of light elements. Indeed there is no obvious reason outside of the Big Bang that, for example, the young universe (i.e. before star formation, as determined by studying matter essentially free of stellar nucleosynthesis products) should have more helium than deuterium or more deuterium than ³He, and in constant ratios, too.

Galactic evolution and distribution

Main article: Large-scale structure of the cosmos

Detailed observations of the morphology and distribution of galaxies and quasars provide strong evidence for the Big Bang. A combination of observations and theory suggest that the first quasars and galaxies formed about a billion years after the Big Bang, and since then larger structures have been forming, such as galaxy clusters and superclusters. Populations of stars have been aging and evolving, so that distant galaxies (which are observed as they were in the early universe) appear very different from nearby galaxies (observed in a more recent state). Moreover, galaxies that formed relatively recently appear markedly different from galaxies formed at similar distances but shortly after the Big Bang. These observations are strong arguments against the steady-state model. Observations of star formation, galaxy and quasar distributions, and larger structures agree well with Big Bang simulations of the formation of structure in the universe and are helping to complete details of the theory.

Features, issues and problems

A number of problems have arisen within the Big Bang theory throughout its history. Some of them are mainly of historical interest today, and have been avoided either through modifications to the theory or as the result of better observations. Other issues, such as the cuspy halo problem and the dwarf galaxy problem of cold dark matter, are not considered to be fatal as they can be addressed through refinements of the theory.

There are a small number of proponents of non-standard cosmologies who doubt that there was a Big Bang at all. They claim that solutions to standard problems in the Big Bang theory involve ad hoc modifications and addenda to the theory. Most often attacked are the parts of standard cosmology that include dark matter, dark energy, and cosmic inflation. However, while explanations for these features remain at the frontiers of inquiry in physics, together they are suggested by independent observations of Big Bang nucleosynthesis, the cosmic microwave background, large scale structure and Type Ia supernovae. The gravitational effects of these features are understood observationally and theoretically but they have not yet been successfully incorporated into the Standard Model of particle physics. Though some aspects of the theory remain inadequately explained by fundamental physics, almost all astronomers and physicists accept that the close agreement between Big Bang theory and observation have firmly established all the basic parts of the theory.

The following is a short list of Big Bang "problems" and puzzles:

Horizon problem

Main article: horizon problem

The horizon problem results from the premise that information cannot travel faster than light, and hence two regions of space which are separated by a greater distance than the speed of light multiplied by the age of the universe cannot be in causal contact. The observed isotropy of the cosmic microwave background (CMB) is problematic in this regard, because the horizon size at that time corresponds to a size that is about 2 degrees on the sky. If the universe has had the same expansion history since the Planck epoch, there is no mechanism to cause these regions to have the same temperature.

A resolution to this apparent inconsistency is offered by inflationary theory in which a homogeneous and isotropic scalar energy field dominates the universe at a time 10^-35 seconds after the Planck epoch. During inflation, the universe undergoes exponential expansion, and regions in causal contact expand so as to be beyond each other's horizons. Heisenberg's uncertainty principle predicts that during the inflationary phase there would be quantum thermal fluctuations, which would be magnified to cosmic scale. These fluctuations serve as the seeds of all current structure in the universe. After inflation, the universe expands according to Hubble's law, and regions that were out of causal contact come back into the horizon. This explains the observed isotropy of the CMB. Inflation predicts that the primordial fluctuations are nearly scale invariant and Gaussian which has been accurately confirmed by measurements of the CMB.

Flatness problem

Main article: flatness problem

The flatness problem is an observational problem that results from considerations of the geometry associated with a Friedmann-Lemaître-Robertson-Walker metric. In general, the universe can have three different kinds of geometries: hyperbolic geometry, Euclidean geometry, or elliptic geometry. The geometry is determined by the total energy density of the universe (as measured by means of the stress-energy tensor): hyperbolic results from a density less than the critical density, elliptic from a density greater than the critical density, and Euclidean from exactly the critical density. The universe is required to be within one part in 10¹⁵ of the critical density in its earliest stages. Any greater deviation would have caused either a Heat Death or a Big Crunch, and the universe would not exist as it does today.

A possible resolution to this problem is again offered by inflationary theory. During the inflationary period, spacetime expanded to such an extent that any residual curvature associated with it would have been smoothed out to a high degree of precision. Thus, it is believed that inflation drove the universe to be very nearly spatially flat.

Magnetic monopoles

The magnetic monopole objection was raised in the late 1970s. Grand unification theories predicted point defects in space that would manifest as magnetic monopoles with a density much higher than was consistent with observations, given that searches have never found any monopoles. This problem is also resolvable by cosmic inflation, which removes all point defects from the observable universe in the same way that it drives the geometry to flatness.

Baryon asymmetry

It is not yet understood why the universe has more matter than antimatter. It is generally assumed that when the universe was young and very hot, it was in statistical equilibrium and contained equal numbers of baryons and anti-baryons. However, observations suggest that the universe, including its most distant parts, is made almost entirely of matter. An unknown process called baryogenesis created the asymmetry. For baryogenesis to occur, the Sakharov conditions, which were laid out by Andrei Sakharov, must be satisfied. They require that baryon number be not conserved, that C-symmetry and CP-symmetry be violated, and that the universe depart from thermodynamic equilibrium. All these conditions occur in the Standard Model, but the effect is not strong enough to explain the present baryon asymmetry. Experiments taking place at CERN near Geneva seek to trap enough anti-hydrogen to compare its spectrum with hydrogen. Any difference would be evidence of a CPT symmetry violation and therefore a Lorentz violation.

Globular cluster age

In the mid-1990s, observations of globular clusters appeared to be inconsistent with the Big Bang. Computer simulations that matched the observations of the stellar populations of globular clusters suggested that they were about 15 billion years old, which conflicted with the 13.7-billion-year age of the universe. This issue was generally resolved in the late 1990s when new computer simulations, which included the effects of mass loss due to stellar winds, indicated a much younger age for globular clusters ^[11]. There still remain some questions as to how accurately the ages of the clusters are measured, but it is clear that these objects are some of the oldest in the universe.

Dark matter

Main article: dark matter

During the 1970s and 1980s various observations (notably of galactic rotation curves) showed that there was not sufficient visible matter in the universe to account for the apparent strength of gravitational forces within and between galaxies. This led to the idea that up to 90% of the matter in the universe is not normal or baryonic matter but rather dark matter. In addition, assuming that the universe was mostly normal matter led to predictions that were strongly inconsistent with observations. In particular, the universe is far less lumpy and contains far less deuterium than can be accounted for without dark matter. While dark matter was initially controversial, it is now a widely accepted part of standard cosmology due to observations of the anisotropies in the CMB, galaxy cluster velocity dispersions, large-scale structure distributions, gravitational lensing studies, and x-ray measurements from galaxy clusters. Dark matter has only been detected through its gravitational signature; no particles that might make it up have yet been observed in laboratories. However, there are many particle physics candidates for dark matter, and several projects to detect them are underway.

Dark energy

Main article: dark energy

In the 1990s, detailed measurements of the mass density of the universe revealed a value that was 30% that of the critical density. Since the universe is very nearly spatially flat, as is indicated by measurements of the cosmic microwave background, about 70% of the energy density of the universe was left unaccounted for. This mystery now appears to be connected to another one: Independent measurements of Type Ia supernovae have revealed that the expansion of the universe is undergoing a non-linear acceleration rather than following strictly Hubble's law. To explain this acceleration, general relativity requires that much of the universe consist of an energy component with large negative pressure. This dark energy is now thought to make up the missing 70%. Its nature remains one of the great mysteries of the Big Bang. Possible candidates include a scalar cosmological constant and quintessence. Observations to help understand this are ongoing. Results from WMAP in 2006 indicate that the universe is 74% dark energy, 22% dark matter, and 4% regular matter (see external link).

The future according to the Big Bang theory

Before observations of dark energy, cosmologists considered two scenarios for the future of the universe. If the mass density of the universe is above the critical density, then the universe would reach a maximum size and then begin to collapse. It would become denser and hotter again, ending with a state that was similar to that in which it started—a Big Crunch. Alternatively, if the density in the universe is equal to or below the critical density, the expansion would slow down, but never stop. Star formation would cease as the universe grows less dense. The average temperature of the universe would asymptotically approach absolute zero. Black holes would evaporate. The entropy of the universe would increase to the point where no organized form of energy could be extracted from it, a scenario known as heat death. Moreover, if proton decay exists, then hydrogen, the predominant form of baryonic matter in the universe today, would disappear, leaving only radiation.

Modern observations of accelerated expansion imply that more and more of the currently visible universe will pass beyond our event horizon and out of contact with us. The eventual result is not known. The ΛCDM model of the universe contains dark energy in the form of a cosmological constant. This theory suggests that only gravitationally bound systems, such as galaxies, would remain together, and they too would be subject to heat death, as the universe cools and expands. Other explanations of dark energy — so-called phantom energy theories — suggest that ultimately galaxy clusters and eventually galaxies themselves will be torn apart by the ever-increasing expansion in a so-called Big Rip.

Speculative physics beyond the Big Bang

While the Big Bang model is well established in cosmology, it is likely to be refined in the future. Little is known about the earliest universe, when inflation is hypothesized to have occurred. There may also be parts of the universe well beyond what can be observed in principle. In the case of inflation this is required: exponential expansion has pushed large regions of space beyond our observable horizon. It may be possible to deduce what happened when we better understand physics at very high energy scales. Speculations about this often involve theories of quantum gravitation.

Some proposals are:

chaotic inflation
brane cosmology models, including the ekpyrotic model in which the Big Bang is the result of a collision between branes
an oscillatory universe in which the early universe's hot, dense state resulted from the Big Crunch of a universe similar to ours. The universe could have gone through an infinite number of big bangs and big crunches. The cyclic extension of the ekpyrotic model is a modern version of such a scenario. (The chief outstanding problem is that entropy would apparently be carried over to each new cycle, resulting in a condition of heat death in the remote past).
models including the Hartle-Hawking boundary condition in which the whole of space-time is finite.

Some of these scenarios are qualitatively compatible with one another. Each entails untested hypotheses.

Philosophical and religious interpretations

There are a number of interpretations of the Big Bang theory that are extra-scientific. Some of these ideas purport to explain the cause of the Big Bang itself (first cause), although science cannot possibly show a first cause, so they have been criticized by some naturalist philosophers as being modern creation myths. Some people believe that the Big Bang theory lends support to traditional views of creation as given in Genesis, for example, while others believe that the Big Bang theory is inconsistent with such views.

The Big Bang, as a scientific theory, is not based on any religion. While some religious interpretations conflict with the Big Bang story of the universe, there are many other interpretations that do not.

The following is a list of various religious interpretations of the Big Bang theory:

A number of Christian churches, the Roman Catholic Church in particular, have accepted the Big Bang as a possible description of the origin of the universe, interpreting it to allow for a philosophical first cause. Pope Pius XII was an enthusiastic proponent of the Big Bang even before the theory was scientifically well established.
Some students of Kabbalah, deism and other non-anthropomorphic faiths concord with the Big Bang theory, for example connecting it with the theory of "divine retraction" (tzimtzum) as explained by the Jewish scholar Moses Maimonides.
Some modern Islamic scholars believe that the Qur'an parallels the Big Bang in its account of creation, described as follows: "Do not the unbelievers see that the heavens and the earth were joined together as one unit of creation, before We clove them asunder?" (Ch:21,Ver:30). The claim has also been made that the Qur'an describes an expanding universe: "The heaven, We have built it with power. And verily, We are expanding it." (Ch:51,Ver:47). Parallels with the Big Crunch and an oscillating universe have also been suggested: "On the day when We will roll up the heavens like the rolling up of the scroll for writings, as We originated the first creation, (so) We shall reproduce it; a promise (binding on Us); surely We will bring it about." (Ch:21,Ver:104).
Certain theistic branches of Hinduism, such as in Vaishnavism, conceive of a theory of creation with similarities to the theory of the Big Bang. The Hindu mythos, narrated for example in the third book of the Bhagavata Purana (primarily, chapters 10 and 26), describes a primordial state which bursts forth as the Great Vishnu glances over it, transforming into the active state of the sum-total of matter ("prakriti"). Other forms of Hinduism assert a universe without beginning or end.
Buddhism has a concept of a universe that has no creation event, but instead goes through infinitely repeated cycles of expansion, stability, contraction, and quiescence. The Big Bang, however, is not seen to be in conflict with this since there are ways to conceive an eternal universe within the paradigm. A number of popular Zen philosophers were intrigued, in particular, by the concept of the oscillating universe.

Notes

↑ R. A. Alpher, H. A. Bethe, G. Gamow, "The Origin of Chemical Elements,"Physical Review 73 (1948), 803.
↑ G. Gamow, Nature 162 (1948), 680.
↑ V. Slipher, paper presented to the American Astronomical Society, (1915).
↑ G. Lemaître, Annals of the Scientific Society of Brussels(1927). In 1929, Edwin Hubble provided an observational basis for Lemaître's theory. He discovered that, relative to the Earth, the galaxies are receding in every direction at speeds directly proportional to their distance from the Earth. This fact is now known as Hubble's law <ref>E. Christianson ''Edwin Hubble: Mariner of the Nebulae''. </li> <li id="_note-4">'''[[#_ref-4|↑]]''' F. Hoyle '"A New Model for the Expanding universe", ''Monthly Notices of the Royal Astronomical Society'', '''108''' (1948), 372.</li> <li id="_note-5">'''[[#_ref-5|↑]]''' A. V. Ivanchik, et al. "The fine-structure constant: a new observational limit on its cosmological variation and some theoretical consequences", ''Astronomy and Astrophysics'' '''343''' (1999) 439.</li> <li id="_note-6">'''[[#_ref-6|↑]]''' J. Goodman ''Physics Review D'', '''52''' (1995) 1821.</li> <li id="_note-7">'''[[#_ref-7|↑]]''' Caltech Submillimeter Observatory has a program underway for measuring detail observations of the CMB to look for Sunyaev-Zel'dovich Effect correlations. [http://www.submm.caltech.edu/cso/]</li> <li id="_note-8">'''[[#_ref-8|↑]]''' D. N. Spergel, et al. "First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters", ''Astrophysical Journal Supplement Series'', '''148''' (2003) 175.</li> <li id="_note-9">'''[[#_ref-9|↑]]''' N.W. Boggess, et al. "The COBE Mission: Its Design and Performance Two Years after the launch," ''Astrophysical Journal'', '''397''' (1992), 420. </li> <li id="_note-10">'''[[#_ref-10|↑]]''' A. A. Navabi and N. Riazi, "Is the Age Problem Resolved?" ''Journal of Astrophysics and Astronomy'' '''24''' (2003), 3.</li></ol></ref>